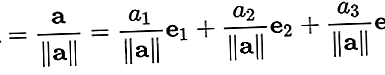Вектор в математиката и физиката може да се определи като геометрични обекти, които имат величина и посока. Векторът е изобразен със стрелка, където основата на стрелката показва точка на улавяне (начална точка) на вектор, дължината на стрелката показва размера или стойността на вектора (колкото по-дълга е стрелката, толкова по-голяма е стойността или стойност на вектора и обратно), докато стрелката показва посоката на вектора.

Писмено, ако векторът започва в точка А и завършва в точка Б, тогава той може да бъде написан с малка буква, над която има линия / стрелка като 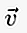 или
или 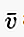 или също:
или също:
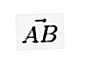
Видове вектори
Векторът в математиката е разделен на 4 вида, включително:
Позиционен вектор
Вектор, чиято начална точка е 0 (0,0), а завършекът му е A (a1, a2).
Нулев вектор
"Вектор нула" (нулев вектор илинулев вектор) е вектор, чиято дължина е "нула". Записът в тази векторна координата е (0,0,0) и обикновено му се дава символ  , или0. Този вектор се различава от другите вектори по това, че не може да бъде нормализиран (т.е. нито един векторен единица не е кратен на нулевия вектор). Броят на векторите е нула с всеки вектора еа (това е,0+а=а).
, или0. Този вектор се различава от другите вектори по това, че не може да бъде нормализиран (т.е. нито един векторен единица не е кратен на нулевия вектор). Броят на векторите е нула с всеки вектора еа (това е,0+а=а).
Нулевият вектор няма ясна посока на вектора.
Единичен вектор
е вектор с дължина "един". Обикновено единичният вектор се използва само за посочване на посоката. Вектор с произволна дължина може да бъде разделен на дължината, за да се получи единичен вектор. Това е известно като "нормализиране" на вектор. Единичният вектор често се обозначава с "капачка" над малката буква "а", както вâ.
За нормализиране на вектора = [а1, а2, а3], разделете вектора на дължината ||а||. Така:
Базов вектор
Единичен вектор, който е перпендикулярен един на друг. В двуизмерен космически вектор (R2) има два основни вектора, а именно 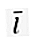 = (1, 0) и
= (1, 0) и 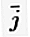 = (0, 1).
= (0, 1).
Прилика на два вектора
Казват се, че два вектора са еднакви, ако имат еднаква дължина и посока

Подравняване на два вектора
Два вектора се наричат успоредни (успоредни), ако линията, представляваща двата вектора, е успоредна.
Векторни операции
Скаларно умножение
Векторът може да бъде умножен по скалар, което води и до вектор, полученият вектор е:
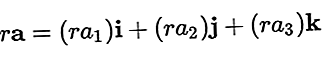
Добавяне на вектор и изваждане на вектор
Като пример за вектор а=а1i + а2j + а3к иб=б1i + б2j + б3к
Резултатът от плюс b е: 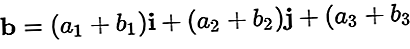
векторната редукция се прилага и чрез замяна на знака + в знак -